Часта ў статыстыцы пры аналізе якога-небудзь з’явы або працэсу неабходна ўлічваць не толькі інфармацыю аб сярэдніх узроўнях доследных паказчыкаў, але і роскід або варыяцыю значэнняў асобных адзінак, якая з’яўляецца важнай характарыстыкай якая вывучаецца сукупнасці.
У найбольшай ступені варыяцыі схільныя курсы акцый, аб’ёмы попыту і прапановы, працэнтныя стаўкі ў розныя перыяды часу і ў розных месцах.
Асноўнымі паказчыкамі, якія характарызуюць варыяцыю, з’яўляюцца размах, дысперсія, сярэдняе квадратическое адхіленне і каэфіцыент варыяцыі.
размах варыяцыі ўяўляе сабой рознасць максімальнага і мінімальнага значэнняў прыкметы: R = Xmax — Xmin. Недахопам гэтага паказчыка з’яўляецца тое, што ён ацэньвае толькі межы вар’іравання прыкметы і не адлюстроўвае яго калыхаў ўнутры гэтых межаў.
дысперсія пазбаўленая гэтага недахопу. Яна разлічваецца як сярэдні квадрат адхіленняў значэнняў прыкметы ад іх сярэдняй велічыні:
Спрошчаны спосаб разліку дысперсіі ажыццяўляецца з дапамогай наступных формул (просты і ўзважанай):
Прыклады прымянення дадзеных формул прадстаўленыя ў задачах 1 і 2.
Шырока распаўсюджаным на практыцы паказчыкам з’яўляецца сярэдняе квадратическое адхіленне:
Сярэдняе квадратическое адхіленне вызначаецца як квадратны корань з дысперсіі і мае тую ж мернасць, што і вывучаецца прыкмета.
Разгледжаныя паказчыкі дазваляюць атрымаць абсалютная значэнне варыяцыі, г.зн. ацэньваюць яе ў адзінках вымярэння доследнага прыкметы. У адрозненне ад іх, каэфіцыент варыяцыі вымярае скаланаецца ў адносным выражэнні — адносна сярэдняга ўзроўню, што ў шматлікіх выпадках з’яўляецца пераважней.
— формула для разліку каэфіцыента варыяцыі.
Прыклады рашэння задач па тэме «Паказчыкі варыяцыі ў статыстыцы»
задача 1. Пры вывучэнні ўплыву рэкламы на памер сярэднямесячнага ўкладу ў банках раёна абследавана 2 банка. Атрыманы наступныя вынікі:
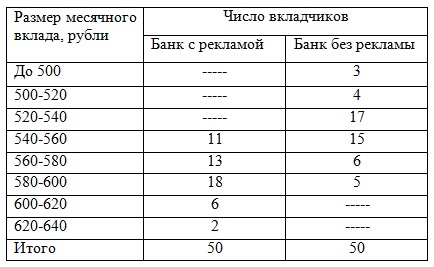
1) для кожнага банка: а) сярэдні памер укладу за месяц; б) дысперсію ўкладу;
2) сярэдні памер укладу за месяц для двух банкаў разам;
3) дысперсіі ўкладу для 2-х банкаў, якая залежыць ад рэкламы;
4) дысперсіі ўкладу для 2-х банкаў, якая залежыць ад усіх фактараў, акрамя рэкламы;
5) Агульную дысперсію выкарыстоўваючы правіла складання;
6) Каэфіцыент дэтэрмінацыі;
7) Карэляцыйныя стаўленне.
1) Складзем разліковую табліцу для банка з рэкламай. Для вызначэння сярэдняга памеру ўкладу за месяц знойдзем сярэдзіны інтэрвалаў. Пры гэтым велічыня адкрытага інтэрвалу (першага) ўмоўна прыраўноўваецца да велічыні інтэрвалу, які прымыкае да яго (другога).
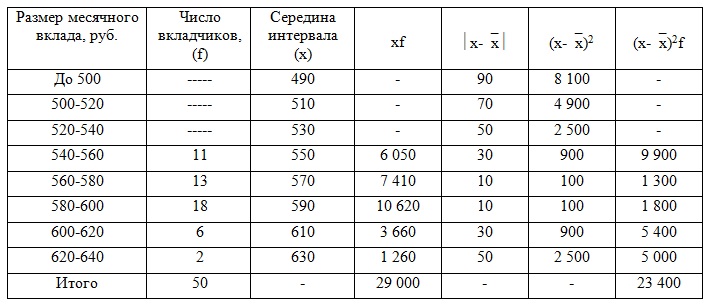
Сярэдні памер укладу знойдзем па формуле сярэдняй арыфметычнай ўзважанай:
= 29 000/50 = 580 руб.
Дысперсію ўкладу знойдзем па формуле:
Аналагічныя дзеянні вырабім для банка без рэкламы:
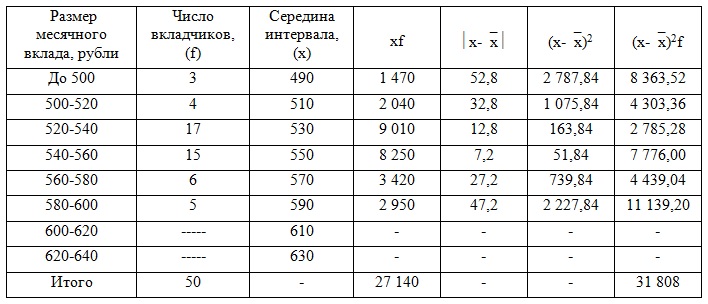
2) Знойдзем сярэдні памер ўкладу для двух банкаў разам. Хср = (580 × 50 + 542,8 × 50) / 100 = 561,4 руб.
3) дысперсіі ўкладу, для двух банкаў, якая залежыць ад рэкламы знойдзем па формуле: #&63; 2 = pq (формула дысперсіі альтэрнатыўнага прыкметы). Тут р = 0,5 — доля фактараў, якія залежаць ад рэкламы; q = 1-0,5, тады #&63; 2 = 0,5 * 0,5 = 0,25.
4) Паколькі доля астатніх фактараў роўная 0,5, то дысперсія ўкладу для двух банкаў, якая залежыць ад усіх фактараў акрамя рэкламы таксама 0,25.
5) Вызначым агульную дысперсію, выкарыстоўваючы правіла складання.
= [(580-561,4) 250+ (542,8-561,4) 250] / 100 = 34 596/100 = 345,96
#&63; 2 = #&63; 2 факт + #&63; 2 ост = 552,08 + 345,96 = 898,04
6) Каэфіцыент дэтэрмінацыі #&51; 2 = #&63; 2 факт / #&63; 2 = 345,96 / 898,04 = 0,39 = 39% — памер ўкладу на 39% залежыць ад рэкламы.
7) Эмпірычнае карэляцыйнае стаўленне #&51; = √ #&51; 2 = √0,39 = 0,62 — сувязь досыць цесная.
задача 2. Маецца групоўка прадпрыемстваў па велічыні таварнай прадукцыі:
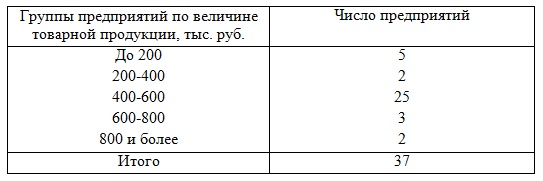
Вызначыць: 1) дысперсію велічыні таварнай прадукцыі; 2) сярэдняе квадратическое адхіленне; 3) каэфіцыент варыяцыі.
1) Па ўмове прадстаўлены інтэрвальныя шэраг размеркавання. Яго неабходна выказаць дыскрэтна, гэта значыць знайсці сярэдзіну інтэрвалу (х ‘). У групах закрытых інтэрвалаў сярэдзіну знойдзем па простай сярэдняй арыфметычнай. У групах з верхняй мяжой — як рознасць паміж гэтай верхняй мяжой і паловай памеру наступнага за ім інтэрвалу (200- (400-200): 2 = 100).
У групах з ніжняй мяжой — сумай гэтай ніжняй мяжы і паловы памеру папярэдняга інтэрвалу (800+ (800-600): 2 = 900).
Разлік сярэдняй велічыні таварнай прадукцыі робім па формуле:
Хср = k × ((#&31;((Х’-a): k) × f): Σf) + a. Тут а = 500 — памер варыянту пры найбольшай частаце, k = 600-400 = 200 — памер інтэрвалу пры найбольшай частаце. Вынік змесцім у табліцу:
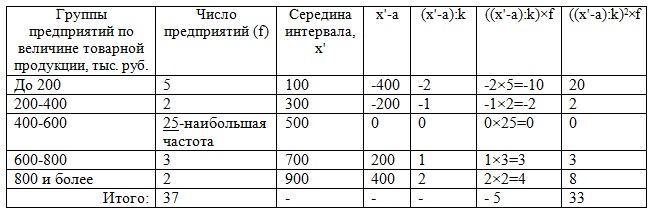
Такім чынам, сярэдняя велічыня таварнай прадукцыі за вывучаецца перыяд у цэлым роўная Хср = (-5: 37) × 200 + 500 = 472,97 тыс. Руб.
2) дысперсія знойдзем па наступнай формуле:
#&63; 2 = (33/37) * 2002- (472,97-500) 2 = 35 675,67-730,62 = 34 945,05
3) сярэдняе квадратическое адхіленне: #&63; = ± √ #&63; 2 = ± √34 945,05 ≈ ± 186,94 тыс. Руб.
4) каэфіцыент варыяцыі: V = (#&63; / Хср) * 100 = (186,94 / 472,97) * 100 = 39,52%
Іншыя артыкулы па дадзенай тэме:
Спіс выкарыстаных крыніц
- Белабародава С.С. і інш. Тэорыя статыстыкі: Тыпавыя задачы з кантрольнымі заданнямі. Екацерынбург: І. ць Урал. дзярж. эканом. ун-та, 2001;
- Минашкин В.Г. і інш. Курс лекцый па тэорыі статыстыкі. / Маскоўскі міжнародны інстытут эканаметрыка, інфарматыкі, фінансаў і правы. — М. 2003;
- Сізова Т.М. Статыстыка: падручнік. — СПб .: СПб ГУИТМО, 2005;
- Фёдарава Л.Н., Фёдарава А.Я. Метадычныя ўказанні па напісанні кантрольнай работы па курсе «Статыстыка» для студэнтаў эканамічных спецыяльнасцяў: УрГЭУ, 2007;
2012-2015 © Лана Забродскі (у Google+). Пры капіяванні матэрыялаў сайта спасылка на крыніцу абавязковая
Задача №48. Разлік паказчыкаў варыяцыі
У інвестара маецца дзве альтэрнатывы ўкладанні грашовых сродкаў у дзейнасць гандлёвых кампаній А і В. Аналіз паказаў, што рэнтабельнасць аналагічных кампаній за апошнія 5 гадоў склала:
Зыходзячы з крытэрыю рызыкі, выберыце і абгрунтуйце найбольш пераважны для інвестара варыянт (разлічыце сярэдняе квадратическое адхіленне і каэфіцыент варыяцыі).
Разлічым сярэдняе значэнне рэнтабельнасці продажаў па формуле сярэдняй арыфметычнай просты:
Пабудуем дапаможную табліцу разліковых дадзеных:
Сярэдняя рэнтабельнасць продажаў для арганізацыі А:
Сярэдняя рэнтабельнасць продажаў для арганізацыі В:
Дысперсія — гэта сярэдняя арыфметычная квадратаў адхіленняў кожнага значэння прыкметы ад сярэдняй арыфметычнай.
Разлік дысперсіі ў дыскрэтных шэрагах размеркавання вырабляецца па формуле:
Сярэдняе квадратическое адхіленне вызначым па формуле:
Каэфіцыент варыяцыі разлічваецца па формуле:
Па велічыні каэфіцыента варыяцыі можна меркаваць аб ступені варыяцыі рэнтабельнасці продажаў. Чым больш яго велічыня, тым больш роскід значэння прыкмет вакол сярэдняй, тым больш рызыкоўная праект.
Ўкладанні грашовых сродкаў у дзейнасць гандлёвай кампаніі А схільныя большай рызыцы, бо каэфіцыент варыяцыі больш і ён вельмі высокі. Таму для ўкладання грашовых сродкаў найбольш пераважны варыянт інвеставання ў дзейнасць гандлёвай кампаніі В.