Базавыя задачы па эканоміцы
1. Лінейная функцыя попыту
ўмова: Дана функцыя попыту Qd(P) = 100 — 2P, знайдзіце кропкавую эластычнасць попыту па цане пры P0 = 20.
рашэнне: Мы можам адразу скарыстацца формулай кропкавай эластычнасці попыту па цане для бесперапыннага выпадкі, так як нам вядомая функцыя попыту па цане: (1) E d p = Q ‘p* P0/ Q0
Для формулы нам спатрэбіцца знайсці вытворную функцыі Qd(P) па параметры P: Q ‘p = (100 — 2P) ‘p = -2. Звярніце ўвагу на адмоўны знак вытворнай. Калі закон попыту выконваецца, то вытворная функцыі попыту па цане заўсёды павінна быць адмоўнай.
Цяпер знойдзем другую каардынату нашага пункту: Q0(P0) = Q0(20) = 100 — 2 * 20 = 60.
Падстаўляем атрыманыя дадзеныя ў формулу (1) і атрымліваем адказ: E d p = -2 * 20/60 = -2/3.
Заўвага: пры вырашэнні дадзенай задачы мы можам таксама скарыстацца формулай эластычнасці попыту па цане для дыскрэтнай выпадку (гл. задачу 5). Для гэтага нам спатрэбіцца зафіксаваць каардынаты кропкі, у якой мы знаходзімся: (Q0,P0) = (60,20) і пралічыць змяненне цаны на 1%, паводле вызначэння: (Q1,P1) = (5,6; 20,2). Падстаўляем усё гэта ў формулу. Адказ атрымліваецца аналагічным: E d p = (59,6 — 60) / (20.2 — 20) * 20/60 = -2/3.
2. Лінейная функцыя попыту (агульны выгляд)
ўмова: Дана функцыя попыту Qd(P) = a — bP, знайдзіце кропкавую эластычнасць попыту па цане пры P = P0.
рашэнне: Зноў скарыстаемся формулай (1) кропкавай эластычнасці попыту па цане для бесперапыннага выпадку.
Вытворная функцыі Qd(P) па параметры P: Q’p = (a — bP) ‘p = -b. Знак зноў адмоўны, гэта добра, значыць мы не дапусцілі памылкі.
Другая каардыната разгляданай кропкі: Q0(P0) = A — b * P0. У выпадку, калі ў формуле прысутнічаюць параметры a і b, ня бянтэжцеся. Яны выконваюць ролю каэфіцыентаў функцыі попыту.
Заўвага: Цяпер, ведаючы універсальную формулу эластычнасці попыту па цане для лінейнай функцыі (2), мы можам падставіць любыя значэнні параметраў a і b, а таксама каардынатаў P0 і Q0, і атрымаць выніковае значэнне E d p.
3. Функцыя попыту з пастаяннай эластычнасцю
ўмова: Дана функцыя попыту Qd(P) = 1 / P, знайдзіце кропкавую эластычнасць попыту па цане пры P = P0.
рашэнне: Яшчэ адзін вельмі распаўсюджаны выгляд функцыі попыту — гіпербала. Кожны раз, калі попыт задаецца функцыянальна, выкарыстоўваецца формула Edp для бесперапыннага выпадку: (1) E d p = Q’p * P0/ Q0
Перш, чым перайсці да вытворнай, неабходна падрыхтаваць зыходную функцыю: Qd(P) = 1 / P = P -1 . тады Q ‘p = (P -1) ‘p = -1 * P -2 = -1 / P 2 . Пры гэтым не забывайце кантраляваць адмоўны знак вытворнай.
Заўвага: Функцыі такога выгляду часта называюцца «Функцыямі з пастаяннай эластычнасць», так як у кожнай кропцы эластычнасць раўняецца пастаяннага значэнні, у нашым выпадку гэта значэнне роўна -1.
4. Функцыя попыту з пастаяннай эластычнасцю (агульны выгляд)
ўмова: Дана функцыя попыту Qd(P) = 1 / P n, знайдзіце кропкавую эластычнасць попыту па цане пры P = P0.
рашэнне: У папярэдняй задачы зададзена гіпербалічныя функцыі попыту. Вырашым яе ў агульным выглядзе, калі ступень функцыі зададзена параметрам .
Запішам зыходную функцыю ў выглядзе: Qd (P) = 1 / P n = P -n . тады Q ‘p = (P -n) ‘p = -n * P -n-1 = -n / P n + 1 . Вытворная адмоўная пры ўсіх неадмо ¢ ных P.
У такім выпадку эластычнасць попыту па цане будзе: Edp = -nP -n-1 * [P / (1 / P n)] = — nP -n-1 * P n + 1 = -n
Заўвага: Мы атрымалі агульны выгляд функцыі попыту з пастаяннай эластычнасцю па цане роўнай .
5. Эластычнасць попыту па цане (дыскрэтны выпадак)
ўмова: Пры дыскрэтным выпадку не дадзена функцыі попыту і змены адбываюцца па кропках. Хай вядома, што калі Q0 = 10, то P0 = 100, а пры Q1 = 9, P1 = 101. Знайдзіце кропкавую эластычнасць попыту па цане.
рашэнне: выкарыстоўваем формулу кропкавай эластычнасці попыту па цане для дыскрэтнай выпадку:
Абавязкова пераконваемся, што атрыманыя значэнні эластычнасці попыту па цане неположительно. Калі яно дадатнае, то 98%, што вы дапусцілі памылку ў вылічэннях і 1%, што вы маеце справу з функцыяй попыту, для якой парушаецца закон попыту.
Заўвага: Паводле азначэння эластычнасці выкарыстанне дадзенай формулы магчыма толькі пры нязначным змене цэны (у ідэале не больш за 1%), ва ўсіх іншых выпадках рэкамендуецца выкарыстоўваць формулу дуговой эластычнасці.
6. Аднаўленне функцыі попыту праз эластычнасць
ўмова: Хай вядома, што калі Q0 = 10, то P0 = 100, а значэнне эластычнасці ў гэтай кропцы роўна -2. Адновіце функцыю попыту на дадзенае карысць, калі вядома, што яна мае лінейны выгляд.
рашэнне: Ўвядзем функцыю попыту ў лінейным выглядзе: Qd(P) = a — bP. У такім выпадку, у пункце (Q0, P0) Эластычнасць будзе роўная Edp = -b * P0/ Q0: Edp = -b * 100/10 = — 10b. Праз гэтыя суадносіны знаходзім, што b = 1/5.
Каб знайсці параметр a, зноў выкарыстоўваем каардынаты кропкі (Q0, P0): 10 = a — 1/5 * 100 -> a = 10 + 20 = 30.
Заўвага: Па падобным прынцыпе можна аднавіць функцыю попыту з пастаяннай цэнавай эластычнасцю.
База задач будзе пастаянна папаўняцца
Прагназаванне попыту і продажаў. запіскі дылетанта
Прагназаванне попыту.
чытаць графікі справа налева усе майстры
Краевугольны камень у кіраванні запасамі і велізарная галаўны боль кіраўніка. Як гэта рабіць на практыцы?
Агульныя развагі пра прагназаванні
Агульныя развагі пра прагназаванні.
Таго, хто не задумваецца аб далёкіх цяжкасцях, абавязкова чакаюць блізкія непрыемнасці
лірычнае адступленне
Удумаемся, адкуль наогул з’явіліся такія паняцці, як верагоднасць, напрыклад? Уся справа ў недастатковасці нашых ведаў аб свеце. Калі мы хочам адказаць на пытанне «які лік выпадзе пры кіданні косткі», нам дастаткова ведаць, якім будзе імпульс, момант кручэння і вышыня над паверхняй у момант адрыву косткі ад рукі. Ну добра, клінічныя педанты могуць яшчэ ўлічыць шчыльнасць паветра, кірунак і сілу ветру і значэнне гравітацыйнай пастаяннай ў дадзенай кропцы прасторы. Але для вызначэння гэтых значэнняў нам у сваю чаргу неабходна дакладна ведаць, якія будуць фактары, якія прыводзяць менавіта да такой паслядоўнасці скарачэння цягліц. Нам жа невядома не толькі якія менавіта фактары ўплываюць на працэс, але і якое колькаснае ўплыў кожнага з іх у асобнасці і іх адвольных камбінацый. Таму адзіным сумленным адказам будзе «адно з шасці магчымых».
Аднак чалавецтва ўсё ж такі хоча большага. Таму з’яўляецца паняцце выпадковасці як меры нашага няведання. Адсюль вынікае адзін важны практычны выснову: чым больш мы зможам ідэнтыфікаваць фактараў, якія ўплываюць на паводзіны выпадковай велічыні, тым менш будзе мера гэтага няведання, гэтай самай выпадковасці. Фактычна менавіта за гэты працэс вызначэння межаў спазнанага і плацяць грошы прагназістаў. У простым выпадку — за фразу «верагоднасць выпадзення 6 складае роўна 1/6». Але на практыцы хутчэй за фразу «паколькі дадзеная костка мае зрушэнне цэнтра цяжару на XX мм пад вуглом YY, размеркаванне верагоднасцяў будзе наступным. ». Менавіта ў такім вывадзе змяшчаецца цалкам практычная каштоўнасць, менавіта тут казіно зарабляюць свае грошы, хоць і не карыстаюцца «кривыми9raquo; косткамі.
Практычная пастаноўка задачы
Не, я зусім не збіраюся пераказваць змесціва падручніка па матстатистике або прагназаванні — на тое ёсць бібліятэка. Гэтыя нататкі хутчэй накіраваны на тое, каб максімальна проста, калі не сказаць прымітыўна, распавесці пра спосабы атрымання адказу на пытанні, звязаныя з неабходнасцю прадказанні паводзінаў велічынь у непасрэднай практычнай жыцця — у прыватнасці, пры кіраванні таварнымі патокамі. Відавочна, што планаванне патокаў немагчыма без ведання меркаванага расходу. Выдатак можа быць любым — продаж у рознічным краме, адгрузка са склада дыстрыбутара ў гандлёвую кропку, адгрузка са склада сыравіны і матэрыялаў у вытворчасць. Так што калі я часам буду для прастаты казаць «продаж» — на самай справе гэта, вядома ж, расход, адгрузка спажыўцу, вонкавым ў адносінах да нашай сістэме. І нас нідзе тут не будзе цікавіць сустрэчны рух грашовага патоку, які замыкае сабой акт продажу. Такім чынам, задача, якую мы будзем вырашаць — прагназаванне попыту на прадукт.
Яшчэ пару слоў пра паняцці, якія будуць выкарыстоўвацца. Калі быць дакладным, у нашай паўсядзённай дзейнасці мы павінны скласці бізнес-прагноз, а не матэматычны. Гэтая велічыня на самай справе можа складацца з некалькіх складнікаў:
незалежны попыт — гэта значыць такое спажыванне, якое адбываецца ў раўнаважкім стане сістэмы, г.зн. нашы спажыўцы не падвяргаюцца вонкавага ўздзеяння тыпу рэкламных акцый, форс-мажорных абставінаў тыпу паводкі або дэфіцыту дадзенага прадукту ў нашых канкурэнтаў.
залежны попыт — астатнія папраўкі, звязаныя з вонкавымі ўздзеяннямі.
Усе далейшыя развагі і абмеркавання метадаў складання прагнозу будуць ставіцца толькі да паводзін менавіта незалежнага попыту, калі іншае не будзе агаворана адмыслова.
Акрамя таго, паколькі мы гаворым пра матэматычным прагназаванні, заснаваным на статыстычных метадах, нам спатрэбяцца дадзеныя аб мінулых адгрузка. Мы будзем меркаваць, што мінулы попыт (факт) складаўся таксама з гэтых двух складнікаў.
І, нарэшце, важны пастулат: залежны попыт у розныя адрэзкі часу можа (павінен, наогул-то) быць розным, аднак незалежны попыт будзе паводзіць сябе падобным чынам як у мінулым, так і ў будучыні. Гэтая здагадка заснавана на ўяўленні аб расходзе як працэсе з унутранага логікай, якая абапіраецца на выразныя паняцці спажывецкай кошту прадукту, памеру рынку і долі кампаніі на ім. Калі гэта здагадка няслушна — што ж, прыйдзецца ісці да цыганкі. Зрэшты, ёсць яшчэ экспертна-калектыўнае прагназаванне, але гэта ўжо па-за рамкамі нашага пытання, хоць у шэрагу выпадкаў экспертная ацэнка — адзіны метад нават пры наяўнасці дастатковых гістарычных дадзеных.
Мы ж зоймемся матэматычнымі метадамі прагназавання. Аднак і тут немагчыма абысціся без удзелу эксперта. Сапраўдны прафесіянал у галіне прагназавання ўмее звесці разам вынікі колькасных метадаў і экспертнае меркаванне. У рэшце рэшт, абгрунтаваныя здагадкі лепш, чым не абгрунтаваныя. Пра гэта мы будзем успамінаць пастаянна, а пакуль завершым старонку цытатай найвядомага Спірас Макридакиса:
Чалавек валодае унікальным веданнем і ўнутранай інфармацыяй, недаступнай колькасных метадаў. Дзіўна, аднак, што эмпірычныя даследаванні і лабараторныя эксперыменты паказалі, што пабудаваныя на іх аснове прагнозы не з’яўляюцца такімі дакладнымі, як тыя, якія атрыманы з дапамогай лікавых метадаў. Чалавек імкнецца быць аптымістам і недаацэньвае ступень нявызначанасці будучыні. Да таго ж кошт прагназавання, выкананага ацэнкавымі метадамі, часта аказваецца значна вышэй, чым пры выкарыстанні колькасных метадаў.
Прагназаванне. Пастаноўка задачы
Любы прагноз заўсёды памылковы. Усё пытанне ў тым, наколькі ён памылковы.
Такім чынам, у нас у распараджэнні ёсць дадзеныя аб продажах. Хай гэта выглядае так:
На мове матэматыкі гэта называецца часовым побач:
Часовай шэраг валодае двума крытычнымі ўласцівасцямі
значэння абавязкова ўпарадкаваны. Перастаўце два любых значэння месцамі, і атрымаеце іншы шэраг
маецца на ўвазе, што значэння ў шэрагу — гэта вынік вымярэння праз аднолькавыя фіксаваныя прамежкі часу; прагназаванне паводзінаў шэрагу азначае атрыманне «продолжения9raquo; шэрагу праз тыя ж самыя прамежкі на зададзены гарызонт прагназавання
Адсюль вынікае патрабаванне да дакладнасці зыходных дадзеных — калі мы хочам атрымаць ПАТЫДНЁВЫ прагноз, зыходная дакладнасць павінна быць не горш, чым патыднёвыя адгрузкі.
Адсюль таксама вынікае, што калі мы «достаем9raquo; з уліковага сістэмы дадзеныя аб продажах памесячна, іх нельга выкарыстоўваць наўпрост, паколькі колькасць часу, на працягу якога вырабляліся адгрузкі, у кожным месяцы рознае і гэта ўносіць дадатковую памылку, паколькі аб’ём продажаў прыблізна прапарцыйны гэтага часу.
Зрэшты, гэта не з’яўляецца такой ужо складанай праблемай — давайце проста прывядзем гэтыя дадзеныя да сярэднядзённага.
Для таго, каб зрабіць нейкія здагадкі адносна далейшага ходу працэсу, мы павінны, як ужо гаварылася, паменшыць ступень нашага няведання. Мы мяркуем, што наш працэс мае нейкія ўнутраныя заканамернасці плыні, зусім аб’ектыўныя ў бягучым асяроддзі. У агульных рысах гэта можна прадставіць як
Y (t) — значэнне нашага шэрагу (напрыклад, аб’ём продажаў) у момант часу t
f (t) — нейкая функцыя, якая апісвае ўнутраную логіку працэсу. Яе ў далейшым будзем называць прагнознай мадэллю
e (t) — шум, памылка, звязаная са выпадковасцю працэсу. Або, што тое ж самае, звязаная з нашым няведаннем, няўменнем ўлічыць іншыя фактары ў мадэлі f (t).
Цяпер наша задача складаецца ў тым, каб адшукаць такую мадэль, каб велічыня памылкі была прыкметна менш назіранай велічыні. Калі мы адшукаем такую мадэль, мы можам лічыць, што працэс у будучыні пойдзе прыкладна ў адпаведнасці з гэтай мадэллю. Больш за тое, чым дакладней мадэль будзе апісваць працэс у мінулым, тым больш у нас упэўненасці, што яна спрацуе і ў будучыні.
Таму працэс як правіла бывае итеративным. Зыходзячы з простага погляду на графік прагназіст выбірае простую мадэль і падбірае яе параметры такім чынам, каб велічыня
была ў нейкім сэнсе мінімальна магчымай. Гэтую велічыню як правіла называюць «остатками9raquo; (Residuals), паколькі гэта тое, што засталося пасля вылічэння мадэлі з фактычных дадзеных, тое, што не ўдалося апісаць мадэллю. Для ацэнкі таго, наколькі добра мадэль апісвае працэс, неабходна палічыць нейкую інтэгральную характарыстыку велічыні памылкі. Найбольш часта для вылічэння гэтай інтэгральнай велічыні памылкі выкарыстоўваюць сярэдняе абсалютнае або сярэднеквадратычнае велічыні рэшткаў па ўсіх t. Калі велічыня памылкі досыць вялікая, спрабуюць «улучшить9raquo; мадэль, г.зн. абраць больш складаны выгляд мадэлі, ўлічыць большую колькасць фактараў. Нам, як практыкам, варта ў гэтым працэсе строга выконваць як мінімум два правілы:
выкарыстанне пэўнай мадэлі павінна быць адназначна вытлумачальна з пункту гледжання здаровага сэнсу. Мы можам паспрабаваць ўвесці ў мадэль продажаў халадзільнікаў у Бабруйску ў якасці фактару надвор’е ў Гандурасе. І, не выключана, атрымаем мадэль з меншай памылкай. Але да таго часу, пакуль мы не можам сфармуляваць, якая можа быць прычынна-следчая сувязь паміж гэтымі велічынямі, такі фактар ўводзіць нельга.
Работа па паляпшэнню якасці прагнозу (паляпшэнню мадэлі) варта цалкам адчувальных грошай. Таму заўсёды неабходна аддаваць сабе справаздачу ў тым, што пачынаючы з нейкага моманту гэтыя намаганні перастаюць папросту акупляцца. Як і ў некаторых іншых выпадках, лепш своечасова спыніцца. Ёсць і іншыя супрацьпаказанні да ўжывання складаных мадэляў. Справа ў тым, што як правіла мадэль для кожнага шэрагу ствараецца і наладжваецца аднойчы, затым толькі часам правяраецца і карэктуецца, тады як прагнозы па гэтай мадэлі ствараюцца на рэгулярнай аснове. Які сэнс, калі пры кожным цыкле складання прагнозу продажаў нам прыйдзецца зноўку даследаваць паводзіны кожнага прадукту і зноўку ствараць для яго мадэлі? Нармальны сістэмны падыход складаецца ў тым, каб аўтаматычна кантраляваць велічыню памылкі прагназавання і па пэўных правілах карэктаваць толькі некаторыя мадэлі. Напрыклад, толькі тыя, у якіх велічыня адноснай памылкі вышэй пэўнага парога І адначасова аб’ём продажаў вышэй пэўнага ўзроўню. Ці проста візуальна ацэньваць дыяграму, падобную гэтай, дзе па вертыкалі адкладзеная велічыня памылкі, а па гарызанталі — цана прадукту.
Наіўныя метады прагназавання
простае сярэдняе
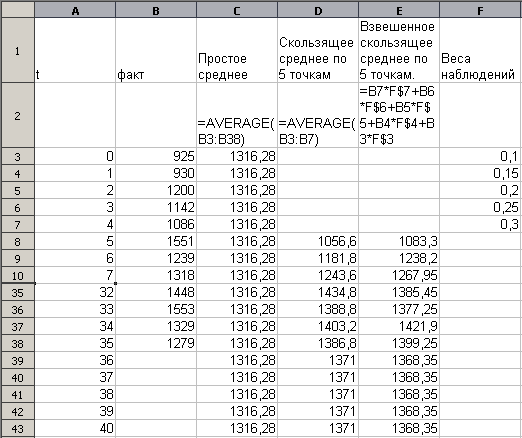
У простым выпадку, калі вымераныя значэння вагаюцца вакол некаторага ўзроўню, відавочным з’яўляецца ацэнка сярэдняга значэння і здагадка аб тым, што і ў далейшым рэальныя продажу будуць вагацца вакол гэтага значэння.
У рэальнасці ж як правіла карцінка хоць трохі, ды «плывет9raquo ;. Кампанія расце, абарот павялічваецца. Адной з мадыфікацый мадэлі сярэдняга, якая ўлічвае гэта з’ява, з’яўляецца адкідванне найбольш старых дадзеных і выкарыстанне для вылічэнні сярэдняга толькі некалькіх k апошніх кропак. Метад атрымаў назву «слізгальнага сярэдняга».
Узважанае слізгальнае сярэдняе
Наступным крокам у мадыфікацыі мадэлі з’яўляецца здагадка аб тым, што пазнейшыя значэння шэрагу больш адэкватна адлюстроўваюць сітуацыю. Тады кожнаму значэнню прысвойваецца вага, тым большы, чым больш свежае значэнне дадаецца.
Для зручнасці можна адразу выбраць каэфіцыенты такім чынам, каб сума іх складала адзінку, тады не прыйдзецца дзяліць. Будзем казаць, што такія каэфіцыенты отнормированы на адзінку.
Вынікі прагназавання на 5 перыядаў наперад па гэтых трох алгарытмах прыведзены ў табліцы
Простае экспанентнае згладжванне
Простае экспанентнае згладжванне
У англамоўнай літаратуры часта сустракаецца абрэвіятура SES — Simple Exponential Smoothing
Адной з разнавіднасцяў метаду асерадненні з’яўляецца метад экспанентна згладжвання. Адрозніваецца ён тым, што шэраг каэфіцыентаў тут выбіраецца зусім пэўным чынам — іх велічыня падае па экспанентным законе. Спынімся тут трохі падрабязней, паколькі метад атрымаў паўсюднае распаўсюджванне дзякуючы прастаце і лёгкасці вылічэнняў.
Хай мы робім прагноз на момант часу t + 1 (на наступны перыяд). Пазначым яго як
Тут мы бярэм у якасці асновы прагнозу прагноз апошняга перыяду, і дадаем папраўку, звязаную з памылкай гэтага прагнозу. Вага гэтай папраўкі будзе вызначаць, наколькі «резко9raquo; наша мадэль будзе рэагаваць на змены. Відавочна, што
Лічыцца, што для павольна змяняецца шэрагу лепш браць значэнне 0.1, а для хутка які змяняецца — падбіраць у раёне 0.3-0.5.
Калі перапісаць гэтую формулу ў іншым выглядзе, атрымліваецца
Мы атрымалі так званае рэкурэнтнага суадносіны — калі наступны член выражаецца праз папярэдні. Цяпер мы прагноз мінулага перыяду выказваем тым жа спосабам праз пазамінулым значэнне шэрагу і гэтак далей. У выніку атрымоўваецца атрымаць формулу прагнозу
У якасці ілюстрацыі прадэманструем згладжванне пры розных значэннях пастаяннай згладжвання
Відавочна, што калі абарот больш-менш манатонна расце, пры такім падыходзе мы будзем сістэматычна атрымліваць заніжаныя лічбы прагнозаў. І наадварот.
Ну і напрыканцы методыка згладжвання з дапамогай электронных табліц. Для першага значэння прагнозу мы возьмем фактычная, а далей па формуле рэкурсіі:
Складнікі прагнознай мадэлі
Відавочна, што калі абарот больш-менш манатонна расце, пры такім «усредняющем9raquo; падыходзе мы будзем сістэматычна атрымліваць заніжаныя лічбы прагнозаў. І наадварот.
Каб больш адэкватна прамадэляваць тэндэнцыю, у мадэль ўводзіцца паняцце «тренда9raquo ;, г.зн. некаторай гладкай крывой, якая больш-менш адэкватна адлюстроўвае «систематическое9raquo; паводзіны шэрагу.
На мал. паказаны той жа шэраг у здагадцы прыблізна лінейнага росту
Такі трэнд называецца лінейным — па выглядзе крывой. Гэта найбольш часта ўжываецца выгляд, радзей сустракаюцца паліномны, экспанентны, лагарыфмічныя трэнды. Выбраўшы выгляд крывой, канкрэтныя параметры звычайна падбіраюць метадам найменшых квадратаў.
Строга кажучы, гэтая кампанента часовага шэрагу называецца трэнд-цыклічнай, то ёсць ўключае ў сябе ваганні з адносна доўгім перыядам, для нашых задач — каля дзесятка гадоў. Гэтая цыклічная складнік характэрная для сусветнай эканомікі ці інтэнсіўнасці сонечнай актыўнасці. Паколькі мы тут вырашаем не такія глабальныя праблемы, гарызонты ў нас паменш, то і цыклічную кампаненту мы пакінем за дужкамі і далей ўсюды будзем казаць аб трэндзе.
Аднак на практыцы нам аказваецца недастаткова мадэляваць паводзіны такім чынам, што мы маем на ўвазе манатонны характар шэрагу. Справа ў тым, што разгляд канкрэтных дадзеных аб продажах запар і побач прыводзіць нас да высновы аб наяўнасці яшчэ адной заканамернасці — перыядычным паўтарэнні паводзін, некаторым шаблоне. Да прыкладу, разглядаючы продажу марожанага, відавочна, што ўзімку яны як правіла ніжэй сярэдняга. Такія паводзіны цалкам зразумела з пункту гледжання здаровага сэнсу, таму ўзнікае пытанне, ці нельга выкарыстоўваць гэтую інфармацыю для памяншэння нашага няведання, для памяншэння нявызначанасці?
Так узнікае ў прагназаванні паняцце «сезоннасці» — любое паўтаральнае праз строга вызначаныя прамежкі часу змена велічыні. Напрыклад, ўсплёск продажаў ёлачных цацак у апошнія 2 тыдні года можна разглядаць як сезоннасць. Як правіла, уздым продажаў супермаркета ў пятніцу і суботу ў параўнанні з астатнімі днямі можна разглядаць як сезоннасць з тыднёвай перыядычнасцю. Хоць і называецца гэтая складнік мадэлі «сезонность9raquo ;, неабавязкова яна звязаная менавіта з сезонам ў бытавым разуменні (вясна, лета). Любая перыядычнасць можа называцца сезоннасцю. З пункту гледжання шэрагу сезоннасць характарызуецца перш за ўсё перыядам або лагам сезоннасці — лікам, праз якое адбываецца паўтор. Напрыклад, калі ў нас шэраг месячных продажаў, мы можам меркаваць, што перыяд складае 12.
Адрозніваюць мадэлі з адытыўная і мультыплікатыўны сезоннасцю. У першым выпадку сезонная папраўка дадаецца да зыходнай мадэлі (у лютым прадаем на 350 адз. Менш, чым у сярэднім)
у другім — адбываецца множанне на каэфіцыент сезоннасці (у лютым прадаем на 15% менш, чым у сярэднім)
Заўважым, што, як ужо гаварылася ў пачатку, само наяўнасць сезоннасці павінна быць вытлумачальна з пункту гледжання здаровага сэнсу. Сезоннасць з’яўляецца следствам і праявай ўласцівасці прадукту (асаблівасцяў яго спажывання ў дадзенай кропцы зямнога шара). Калі мы зможам акуратна ідэнтыфікаваць і вымераць гэта ўласцівасць гэтага канкрэтнага прадукту, мы зможам быць упэўнены, што такія ваганні працягнуцца і ў будучыні. Пры гэтым адзін і той жа прадукт цалкам можа мець розныя характарыстыкі (профілі) сезоннасці ў залежнасці ад месца, дзе ён спажываецца. Калі ж мы не можам растлумачыць такія паводзіны з пункту гледжання здаровага сэнсу, у нас няма падстаў для меркаванага паўтарэння такога шаблону ў будучыні. У гэтым выпадку мы павінны шукаць іншыя фактары, знешнія па адносінах да прадукту і разглядаць іх наяўнасць у будучыні.
Важна тое, што пры выбары трэнду мы павінны выбіраць простую аналітычную функцыю (гэта значыць такую, якую можна выказаць простай формулай), тады як сезоннасць як правіла выяўляецца таблічнай функцыяй. Самы распаўсюджаны выпадак — гадавая сезоннасць з 12 перыядамі па ліку месяцаў — гэта табліца з 11 мультыплікатыўны каэфіцыентаў, якія прадстаўляюць папраўку адносна аднаго апорнага месяца. Або 12 каэфіцыентаў адносна сярэднямесячнага значэння, толькі вельмі важна, што пры гэтым незалежнымі застаюцца тыя ж 11, паколькі 12й адназначна вызначаецца з патрабаванні
Сітуацыя, калі ў мадэлі прысутнічае M статыстычна незалежных (!) Параметраў, у прагназаванні называецца мадэллю з M ступенямі волі. Так што калі вам сустрэнецца адмысловы софт, у якім як правіла неабходна ў якасці ўваходных параметраў задаць лік ступеняў свабоды, гэта адсюль. Напрыклад, мадэль з лінейным трэндам і перыядам 12 месяцаў, будзе мець 13 ступеняў свабоды — 11 ад сезоннасці і 2 ад трэнду.
Як жыць з гэтымі складнікамі шэрагу, разгледзім у наступных частках.
Класічная сезонная декомпозиция
Декомпозиция шэрагу продажаў.
Такім чынам, мы вельмі часта можам назіраць паводзіны шэрагу продажаў, у якім прысутнічаюць кампаненты трэнду і сезоннасці. Мы маем намер палепшыць якасць прагнозу, улічваючы гэтыя веды. Але для таго, каб выкарыстоўваць гэтую інфармацыю, нам неабходныя колькасныя характарыстыкі. Тады мы з фактычных дадзеных зможам выключыць трэнд і сезоннасць і тым самым значна паменшыць велічыню шуму, а значыць і нявызначанасць будучыні.
Працэдура вылучэння невыпадковых кампанент мадэлі з фактычных дадзеных называецца декомпозицией.
Першае, чым мы зоймемся на нашых дадзеных — сезонная декомпозиция, г.зн. вызначэнне лікавых значэнняў сезонных каэфіцыентаў. Для пэўнасці возьмем найбольш распаўсюджаны выпадак: дадзеныя аб продажах згрупаваныя памесячна (паколькі патрабуецца прагноз з дакладнасцю да месяца), мяркуецца лінейны трэнд і мультыплікатыўны сезоннасць з лагам 12.
Згладжваннем называецца працэс, пры якім зыходны шэраг замяняецца іншым, больш плыўным, а заснаваныя на зыходным. Мэтай такога працэсу з’яўляецца ацэнка агульных тэндэнцый, трэнду ў шырокім сэнсе. Метадаў (як і мэтаў) згладжвання існуе шмат, найбольш распаўсюджаныя
ўзбуйненне часовых інтэрвалаў. Відавочна, што шэраг продажаў, агрэгаваных памесячна, паводзіць сябе больш гладка, чым шэраг, заснаваны на дзённых продажах
слізгальнае сярэдняе. Мы ўжо разглядалі гэты метад, калі гаварылі пра наіўных метадах прагназавання
аналітычнае выраўноўванне. У гэтым выпадку зыходны шэраг замяняецца некаторай гладкай аналітычнай функцыяй. Выгляд і параметры падбіраюцца экспертна па мінімуму памылак. Зноў жа, мы гэта ўжо абмяркоўвалі, калі гаварылі аб трэндах
Далей мы будзем выкарыстоўваць згладжванне метадам слізгальнага сярэдняга. Ідэя складаецца ў тым, што набор з некалькіх кропак мы замяняем адной па прынцыпе «цэнтра мас» — значэнне роўна сярэдняму гэтых кропак, а размешчаны цэнтр мас, як няцяжка здагадацца, у цэнтры адрэзка, адукаванага крайнімі кропкамі. Так мы ўсталёўваем нейкі «средний9raquo; ўзровень для гэтых кропак.
У якасці ілюстрацыі наш зыходны шэраг, згладжаны па 5 і 12 кропках:
Як няцяжка здагадацца, калі адбываецца асерадненні па цотная колькасць кропак, цэнтр мас падае ў прамежак паміж кропкамі:
Да чаго гэта я ўсё вяду?
Для таго, каб правесці сезонную декомпозицию, класічны падыход прапануе спачатку правесці згладжванне шэрагу з акном, у дакладнасці супадальным з лагам сезоннасці. У нашым выпадку лаг = 12, так што калі мы згладзім па 12 кропках, па ўсёй бачнасці, абурэння, звязаныя з сезоннасцю, нівеліруюцца і мы атрымаем агульны сярэдні ўзровень. Вось тады ўжо мы пачнем параўноўваць фактычныя продажу з згладжанымі значэннямі — для адытыўная мадэлі будзем адымаць з факту згладжаны шэраг, а для мультыплікатыўны — дзяліць. У выніку атрымаем набор каэфіцыентаў, для кожнага месяца па некалькі штук (у залежнасці ад даўжыні шэрагу). Калі згладжванне прайшло паспяхова, гэтыя каэфіцыенты будуць мець не занадта вялікі роскід, так што асерадненні для кожнага месяца будзе не гэтак ужо дурной задумай.
Два моманты, якія важна адзначыць.
- Асерадненне каэфіцыентаў можна рабіць як вылічэннем стандартнага сярэдняга, так і медыяны. Апошні варыянт вельмі рэкамендуецца многімі аўтарамі, паколькі медыяна не так моцна рэагуе на выпадковыя выкіды. Але мы ў нашай вучэбнай задачы будзем выкарыстоўваць простае сярэдняе.
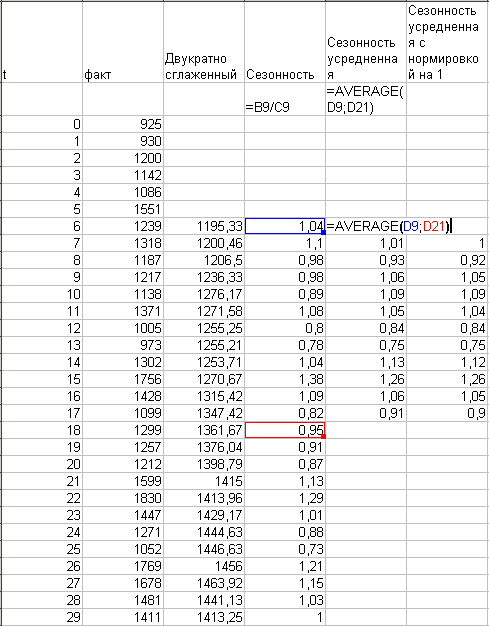
- У нас будзе лаг сезоннасці 12, цотны. Таму нам прыйдзецца зрабіць яшчэ адно згладжванне — замяніць дзве суседнія пункту згладжанымі ў першы раз шэрагу на сярэдняе, тады мы трапім на канкрэтны месяц
На малюнку вынік паўторнага згладжвання:
Цяпер дзелім факт на гладкі шэраг:
На жаль, у мяне былі дадзеныя толькі за 36 месяцаў, а пры згладжванне па 12 кропках адзін год, адпаведна, губляецца. Таму на дадзеным этапе я атрымаў каэфіцыенты сезоннасці толькі па 2 на кожны месяц. Але рабіць няма чаго, гэта лепш, чым нічога. Будзем усредняет гэтыя пары каэфіцыентаў:
Зараз успамінаем, што сума мультыплікатыўны каэфіцыентаў сезоннасці павінна быць = 12, паколькі сэнс каэфіцыента — стаўленне продажаў месяца да сярэднямесячнага. Менавіта гэта робіць апошняя калонка:
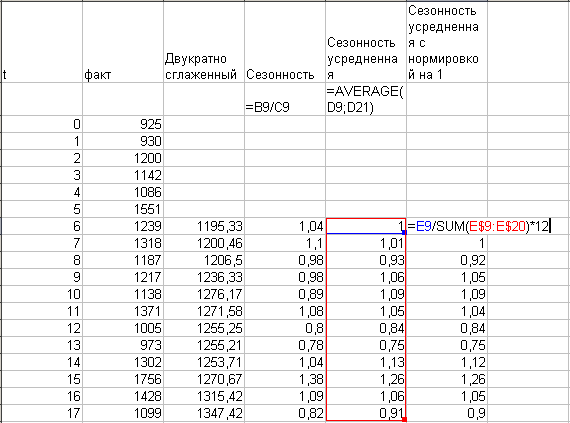
Вось зараз мы выканалі класічную сезонную декомпозицию, гэта значыць атрымалі значэння 12-ці мультыплікатыўны каэфіцыентаў. Зараз прыйшла пара заняцца нашым лінейным трэндам. Для ацэнкі трэнду мы ліквідуем з фактычных продажаў сезонныя ваганні, падзяліўшы факт на атрыманае для дадзенага месяца значэнне.
Цяпер пабудуем на графіцы дадзеныя з ухіленых сезоннасцю, правядзем лінейны трэнд і складзем для цікавасці прагноз на 12 перыядаў наперад як твор значэння трэнду ў кропцы на адпаведны каэфіцыент сезоннасці
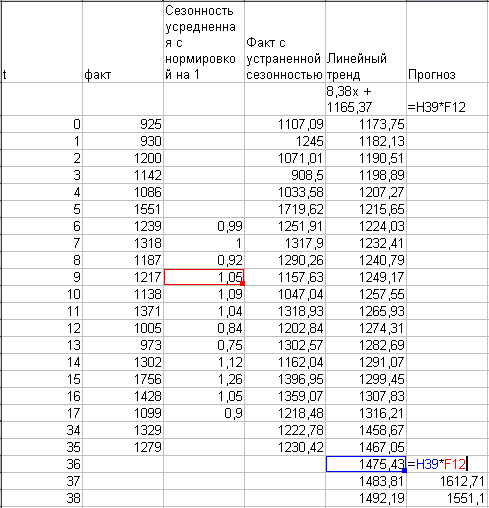
Як відаць з карцінкі, вычышчаныя ад сезоннасці дадзеныя не вельмі добра ўкладваюцца ў лінейную залежнасць — занадта вялікія адхіленні. Магчыма, калі почисить зыходныя дадзеныя ад выкідаў, усё стане нашмат лепш.
Для больш дакладнага вызначэння сезоннасці пры дапамозе класічнай декомпозиции вельмі пажадана мець не менш за 4-5 поўных цыклаў дадзеных, так як адзін цыкл не ўдзельнічае ў вылічэнні каэфіцыентаў.
Што рабіць, калі па тэхнічных прычынах такіх дадзеных няма? Трэба знайсці метад, які не будзе адкідаць ніякую інфармацыю, будзе выкарыстаць усю наяўную для ацэнкі сезоннасці і трэнду. Паспрабуем такі метад разгледзець у наступнай частцы
Экспанентнае згладжванне з улікам трэнду і сезоннасці. Метад Холта-Винтерса
Вяртаючыся да экспанентным згладжванню.
У адной з папярэдніх частак мы ўжо разглядалі простае экспанентнае згладжванне. Нагадаем ў двух словах асноўную ідэю. Мы меркавалі, што прагноз для кропкі t вызначаецца некаторым сярэднім узроўнем папярэдніх значэнняў. Прычым спосаб, якім вылічаецца прагнознае значэнне, вызначаецца рэкурэнтнага суадносінамі
У такім выглядзе метад дае легкатраўнай вынікі, калі шэраг продажаў дастаткова стацыянар — няма выяўленага трэнду або сезонных ваганняў. Але на практыцы такі выпадак — шчасце. Таму мы разгледзім мадыфікацыю дадзенага метаду, якая дазваляе працаваць з трэндавымі і сезоннымі мадэлямі.
Метад атрымаў назву Холта-Винтерса па імёнах распрацоўшчыкаў: Холт прапанаваў метад уліку трэнду, Винтерс дадаў сезоннасць.
Для таго, каб не толькі разабрацца з арыфметыкай, але і «почувствовать9raquo ;, як гэта працуе, давайце трохі звернем нашу галаву і падумаем, што змяняецца, калі мы ўводзім трэнд. Калі для простага экспанентна згладжвання адзнака прагнозу на p-й перыяд рабілася як
дзе Lt — асераднёны па вядомым правілу «агульны ўзровень», то пры наяўнасці трэнду з’яўляецца папраўка
гэта значыць да агульнага ўзроўню дадаецца адзнака трэнду. Прычым як агульны ўзровень, так і трэнд мы будзем усредняет незалежна па метадзе экспанентна згладжвання. Што разумеецца пад асерадненнем трэнду? Мы мяркуем, што ў нашым працэсе прысутнічае лакальны трэнд, які вызначае сістэматычнае прырашчэнне на адным кроку — паміж кропкамі t і t-1, напрыклад. І калі для лінейнай рэгрэсіі лінія трэнду праводзіцца па ўсёй сукупнасці кропак, мы лічым, што пазнейшыя пункту павінны ўносіць большы ўклад, паколькі рынкавае асяроддзе пастаянна змяняецца і больш свежыя дадзеныя больш каштоўныя для прагнозу. У выніку Холт прапанаваў выкарыстаць ужо два рэкурэнтнага суадносін — адно згладжвае агульны ўзровень шэрагу, іншае згладжвае трэндавымі складнік.
Методыка згладжвання такая, што спачатку выбіраюцца пачатковыя значэння ўзроўню і трэнду, а затым робіцца праход па ўсім шэрагу, на кожным кроку вылічаючы новыя значэння па формулах. З агульных меркаванняў зразумела, што пачатковыя значэнні павінны неяк вызначацца зыходзячы з значэнняў шэрагу ў самым пачатку, аднак дакладных крытэрыяў тут няма, прысутнічае элемент валюнтарызму. Найбольш часта выкарыстоўваюцца два падыходу ў выбары «кропак адліку»:
Пачатковы ўзровень роўны першаму значэнні шэрагу, пачатковы трэнд роўны нулю.
Бярэм першыя некалькі кропак (штук 5), праводзім лінію рэгрэсіі (ax + b). Пачатковы ўзровень задаем як b, пачатковы трэнд як a.
Па вялікім рахунку гэтае пытанне не з’яўляецца прынцыповым. Як мы памятаем, ўклад ранніх кропак мізэрны, паколькі каэфіцыенты вельмі хутка (па экспаненце) меншаюць, так што пры дастатковай даўжыні шэрагу зыходных дадзеных мы хутчэй за ўсё атрымаем практычна ідэнтычныя прагнозы. Розніца, аднак, можа праявіцца пры ацэнцы памылкі мадэлі.
На гэтым малюнку паказаны вынікі згладжвання пры двух выбарах пачатковых значэнняў. Тут добра відаць, што вялікая памылка другога варыянту звязана з тым, што пачатковая значэнне трэнду (узятае па 5 кропках) атрымалася яўна завышаным, паколькі мы не ўлічвалі рост, звязаны з сезоннасцю.
Таму (услед за спадаром Винтерсом) ускладніўся мадэль і будзем рабіць прагноз з улікам сезоннасці:
У дадзеным выпадку мы, як і раней, мяркуем мультыплікатыўны сезоннасць. Тады наша сістэма раўнанняў згладжвання атрымлівае яшчэ адну складнік:
дзе s — лаг сезоннасці.
І зноў заўважым, што выбар пачатковых значэнняў, як і велічынь пастаянных згладжвання — пытанне волі і меркаванні эксперта.
Для сапраўды важных прагнозаў, аднак, можна прапанаваць скласці матрыцу ўсіх камбінацый пастаянных і пераборам выбраць такія, якія даюць меншую памылку. Пра метады ацэнкі памылковасці мадэляў мы пагаворым крыху пазней. А пакуль зоймемся згладжваннем нашага шэрагу па метадзе Холта-Винтерса. Пачатковыя значэння будзем у дадзеным выпадку вызначаць па наступным алгарытме:
Бярэм першыя 12 кропак шэрагу, каб нівеліраваць сезоннасць.
Праводзім лінію рэгрэсіі
Задаем пачатковае значэнне ўзроўню 1021,41
Задаем пачатковае значэнне трэнду 26,24
Задаем пачатковыя значэння 12ти сезонных каэфіцыентаў як факт, дзелены на значэнне рэгрэсіі ў кропцы
Цяпер пачатковыя значэння вызначаны.
- Ідзем па працэдуры, атрымліваючы згладжаны ўзровень
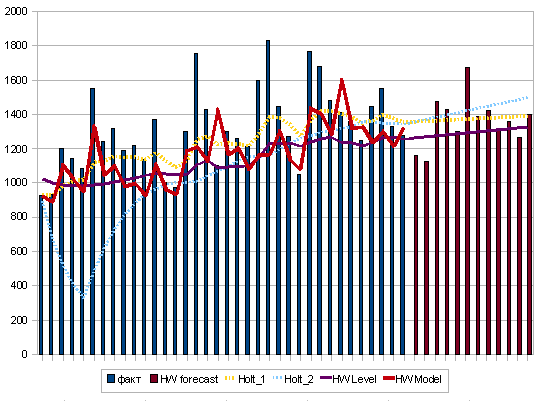
Для цікавасці намалюем мадэль з улікам сезоннасці
Ствараем прагноз ўзроўню на 12 кропак наперад
І прагноз з улікам сезоннасці
Вынікі ўсяго гэтага бязладдзя:
Прагназаванне рэдкіх продажаў. метад Кростона
Прагназаванне рэдкіх продажаў.
Уся вядомая матэматыка прагназавання, якую з задавальненнем апісваюць аўтары падручнікаў, грунтуецца на спадзяванні, што продажу ў пэўным сэнсе "ровные9quot ;. Менавіта пры такой малюначку ў прынцыпе ўзнікаюць такія паняцці, як трэнд або сезоннасць.
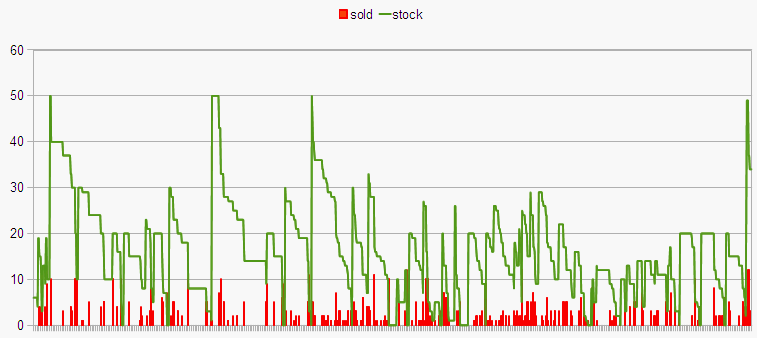
А што рабіць, калі продажу выглядаюць наступным чынам?
Кожны слупок тут — продажу за перыяд, паміж імі продажаў няма, хоць тавар прысутнічае.
Пра якія "трендах9quot; тут можна казаць, калі каля паловы перыядаў маюць нулявыя продажу? І гэта яшчэ не самы клінічны выпадак!
Ужо з саміх графікаў відаць, што трэба прыдумляць нейкія іншыя алгарытмы прадказанні. Хочацца яшчэ заўважыць, што гэтая задача не высмактаная з пальца і не з’яўляецца нейкай рэдкай. Практычна ўсе aftermarket нішы маюць справу менавіта з гэтым выпадкам — аўтазапчасткі, аптэкі, забеспячэнне сэрвісных цэнтраў.
Будзем вырашаць чыста прыкладную задачу. У мяне ёсць дадзеныя аб продажах гандлёвай кропкі з дакладнасцю да дзён. Тэрмін рэакцыі сістэмы паставак хай будзе роўна адзін тыдзень. Задача-мінімум — спрагназаваць хуткасць продажаў. Задача-максімум — вызначыць велічыню страхавога запасу зыходзячы з ўзроўню абслугоўвання ў 95%.
Аналізуючы фізічную прыроду працэсу, Кростон (Croston, J.D.) выказаў здагадку, што
- усе продажу статыстычна незалежныя
- здарылася продаж або няма, падпарадкоўваецца размеркаванні Бярнулі
(З верагоднасцю p падзея адбываецца, з верагоднасцю 1-p няма)
Гэта азначае, што выніковае размеркаванне мае такі выгляд:
Як бачым, ад "колокола9quot; Гаўса гэтая карцінка моцна адрозніваецца. Больш за тое, вяршыня намаляванага ўзгорка адпавядае куплі 25 адзінак, тады як калі мы "у лоб" палічым сярэдняе па шэрагу продажаў, атрымаем 18 адзінак, а разлік СКО дае 16. Адпаведная "нормальная9quot; крывая намаляваная тут зялёным.
Кростон прапанаваў рабіць ацэнку двух незалежных велічынь — перыяду паміж пакупкамі і ўласна памеру пакупкі. Паглядзім на тэставыя дадзеныя, у мяне як раз выпадкова пад рукамі дадзеныя аб рэальных продажах:
Цяпер падзелім зыходны шэраг на два рады па наступных прынцыпах.
Цяпер да кожнага з атрыманых шэрагаў выкарыстоўваецца і ў дачыненні простае экспанентнае згладжванне і атрымаем чаканыя значэння інтэрвалу паміж пакупкамі і велічыні пакупкі. А падзяліўшы другое на першае, атрымаем чаканую інтэнсіўнасць попыту ў адзінку часу.
Так, у мяне ёсць тэставыя дадзеныя па дзённым продажах. Вылучэнне шэрагаў і згладжванне з малым значэннем сталай дало мне
- чаканы перыяд паміж пакупкамі 5.5 дзён
- чаканы памер куплі 3.7 адзінак
такім чынам тыднёвы прагноз продажаў складзе 3.7 / 5.5 * 7 = 4.7 адзінак.
Наогул-то гэта ўсё, што нам дае метад Кростона — кропкавую ацэнку прагнозу. На жаль, гэтага недастаткова для разліку патрэбнага страхавога запасу.
Метад Кростона. Ўдакладненне алгарытму.
Недахоп метаду Кростона.
Праблема наогул-то ўсіх класічных метадаў складаецца ў тым, што яны мадэлююць паводзіны з дапамогай нармальнага размеркавання. І тут сядзіць сістэматычная памылка, паколькі нармальнае размеркаванне мяркуе, што выпадковая велічыня можа змяняцца ад мінус бясконцасці да плюс бясконцасці. Але гэта невялікая бяда для дастаткова рэгулярнага попыту, калі каэфіцыент варыяцыі невялікі, а значыць і верагоднасць з’яўлення адмоўных значэнняў гэтак малаважная, што мы цалкам можам на гэта зачыняць вочы.
Іншая справа — прагназаванне рэдкіх падзей, калі матожидание памеру куплі мае малое значэнне, а СКО пры гэтым цалкам можа апынуцца як мінімум такога ж парадку:
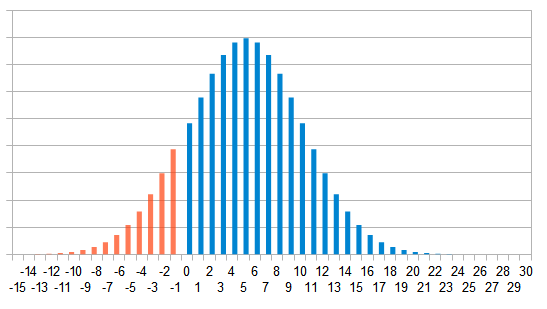
Каб адысці ад такой відавочнай хібнасці, было прапанавана карыстацца логнормальным размеркаваннем, як больш "логично9quot; што апісвае карціну свету:
Калі кагосьці бянтэжаць ўсякія страшныя словы, не хвалюйцеся, прынцып вельмі просты. Бярэцца зыходны шэраг, ад кожнага значэння бярэцца натуральны лагарыфм, і мяркуецца, што атрыманы шэраг ужо паводзіць сябе як нармальна размеркаваны з усёй стандартнай матэматыкай, апісанай вышэй.
Метад Кростона і страхавой запас. Функцыя размеркавання попыту.
Сеў я тут і задумаўся. Ну добра, атрымаў я характарыстыкі патоку попыту:
чаканы перыяд паміж пакупкамі 5.5 дзён
чаканы памер куплі 3.7 адзінак
чаканая інтэнсіўнасць попыту 3.7 / 5.5 адзінак у дзень.
хай я нават атрымаў СКО дзённага попыту для ненулявога продажаў — 2.7. А што там наконт страхавога запасу?
Як вядома, страхавы запас павінен забяспечыць наяўнасць тавару пры адхіленні продажаў ад сярэдняга з пэўнай верагоднасцю. Метрыкі ўзроўню абслугоўвання мы ўжо абмяркоўвалі, давайце для пачатку пагаворым пра ўзровень першага роду. Строгая фармулёўка задачы гучыць так:
У нашай сістэмы паставак ёсць час рэакцыі. Сумарны попыт на тавар за гэты час ёсць велічыня выпадковая, якая мае сваю функцыю размеркавання. ўмова "верагоднасць необнуления запасу" можна запісаць як
У выпадку рэдкіх продажаў функцыя размеркавання можа быць запісаная наступным чынам:
q — верагоднасць нулявога зыходу
p = 1-q — верагоднасць ненулявога зыходу
f (x) — шчыльнасць размеркавання памеру пакупкі
Заўважце, у сваім даследаванні ў папярэдні раз усе гэтыя параметры я вымяраў для дзённага шэрагу продажаў. Таму калі час рэакцыі ў мяне таксама роўна аднаму дню, то гэтую формулу можна паспяхова прымяніць прама адразу. напрыклад:
выкажам здагадку, што f (x) — нармальная.
выкажам здагадку, што ў вобласці x<= 0 верагоднасці, апісваныя функцыяй вельмі нізкія, г.зн.
тады інтэграл ў нашай формуле шукаецца па табліцы Лапласа.
у нашым прыкладзе p = 1 / 5.5, так што
алгарытм пошуку становіцца відавочным — задаўшы SL, нарошчваем k, пакуль F не перавысіць зададзены ўзровень.
Дарэчы, у апошняй калонцы што? Правільна, узровень абслугоўвання другога роду, адпаведны зададзенаму запасе. І тут, як я ўжо казаў, сядзіць некаторы метадалагічны неспадзяванка. Давайце прадставім сабе, што продажы адбываюцца прыблізна з частатой адзін раз у. ну хай будзе 50 дзён. І яшчэ уявім сабе, што мы трымаем нулявы запас. Які ўзровень абслугоўвання будзе? Накшталт як нулявы — няма запасу, няма і абслугоўвання. Тую ж лічбу нам дасць і сістэма кантролю запасу, паколькі назіраецца пастаянны out of stock. Але ж з пункту гледжання банальнай эрудыцыі ў 49 выпадках з 50 продаж дакладна адпавядае попыту. Гэта значыць не прыводзіць да страт прыбытку і лаяльнасці кліентаў, а ні для чаго іншага ўзровень сэрвісу і не прызначаны. Гэты некалькі выраджаных выпадак (чую, спрэчка пачнецца) з’яўляецца проста ілюстрацыяй таго, чаму нават вельмі малы запас пры рэдкім попыце дае высокія ўзроўні сэрвісу.
Але гэта ўсё кветачкі. А што, калі ў мяне змяніўся пастаўшчык, і цяпер час рэакцыі стала раўняцца тыдні, напрыклад? Ну, тут усё становіцца зусім вясёлым, тым, хто не любіць "многаформул9quot ;, рэкамендую далей не чытаць, а чакаць артыкул пра метад Виллемейна.
Наша задача складаецца цяпер у тым, каб прааналізаваць суму продажаў за перыяд рэакцыі сістэмы, зразумець яе размеркаванне, і ўжо адтуль выцягваць залежнасць ўзроўню сэрвісу ад велічыні запасу.
Такім чынам, функцыя размеркавання попыту за адзін дзень і ўсе яе параметры нам вядомыя:
Па-ранейшаму вынік аднаго дня статыстычна незалежны ад любога іншага.
Хай выпадковае падзея складаецца ў тым, што за n дзён здарылася роўна m фактаў ненулявога продажаў. Згодна з законам Бярнулі (ды добра, я ж сяджу і з падручніка спісвае!) Верагоднасць такой падзеі
дзе — лік спалучэнняў з n па m, а p і q — ізноў тыя ж верагоднасці.
Тады верагоднасць таго, што сума прададзенага за n дзён у выніку роўна m фактаў продажаў не перавысіць велічыні z, складзе
дзе — размеркаванне сумы прададзенага, то ёсць скрутка m аднолькавых размеркаванняў.
Ну і паколькі шуканы вынік (сумарныя продажу не перавышаюць z) можа быць атрыманы пры любых m, засталося прасумаваць адпаведныя верагоднасці:
(Першае складнік адпавядае верагоднасці нулявога зыходу усіх n выпрабаванняў).
Што-то далей мне лень з усім гэтым важдацца, жадаючыя могуць самастойна пабудаваць табліцу, аналагічную вышэйпрыведзенай ва ўжыванні да нармальнай шчыльнасці верагоднасці. Для гэтага трэба толькі ўзгадаць, што скрутка m нармальных рапределений з параметрамі (a, s 2) дае нармальнае жа размеркаванне з параметрамі (ma, ms 2).
Прагназаванне рэдкіх продажаў. Метад Виллемейна.
Што дрэннага ў метадзе Кростона?
Справа ў тым, што па-першае, ён мае на ўвазе нармалёвасць размеркавання памеру пакупкі. Па-другое, для адэкватных вынікаў гэта размеркаванне павінна мець невысокую дысперсію. Па-трэцяе, хоць гэта і не так смяротна, прымяненне экспанентна згладжвання для знаходжання характарыстык размеркавання няяўна мае на ўвазе нестацыянарнага працэсу.
Ну ды бог з ім. Для нас самае важнае — рэальныя продажу нават блізка не выглядаюць нармальнымі. Менавіта гэтая думка падштурхнула Виллемейна (Thomas R. Willemain) і кампанію да стварэння больш універсальнага спосабу. А патрэба ў такім метадзе была прадыктавана чым? Правільна, неабходнасцю прагназаваць патрэба ў запасных частках, асабліва ў аўтамабільных запчастках.
Сутнасць падыходу складаецца ва ўжыванні працэдуры бутстраппинга (bootstrapping). Слоўца гэта нарадзілася з старой прымаўкі "pull oneself over a fence by one’s bootstraps", Што амаль літаральна адпавядае нашаму "выцягнуць сябе за ўласныя валасы". Кампутарны тэрмін boot, дарэчы, таксама адсюль. І сэнс гэтага слова ў тым, што нейкая сутнасць змяшчае ў сабе неабходныя рэсурсы, каб саму сябе перавесці ў іншы стан, і пры неабходнасці такую працэдуру магчыма запусціць. Менавіта такі працэс адбываецца з кампутарам, калі мы націскаем на пэўную кнопку.
Ва ўжыванні ж да нашай вузкай задачы працэдура бутстраппинга азначае вылічэнне ўнутраных заканамернасцяў, якія прысутнічаюць у дадзеных, і выконваецца наступным чынам.
Па ўмовах нашай задачы час рэакцыі сістэмы 7 дзён. Мы НЕ ведаем і НЕ ПЫТАЕМСЯ выказаць здагадку выгляд і параметры крывой размеркавання.
Замест гэтага мы з усяго шэрагу 7 разоў выпадкова "выдергиваем9quot; дні, сумуецца продажу гэтых дзён і запісваем вынік.
Паўтараем гэтыя дзеянні, кожны раз запісваючы суму продажаў за 7 дзён.
Пажадана вырабіць вопыт досыць шмат разоў, каб атрымаць найбольш адэкватную карцінку. 10 — 100 тысяч разоў будзе вельмі нядрэнна. Тут вельмі важна, каб дні выбіраліся выпадкова раўнамерна ва ўсім аналізаваным дыяпазоне.
У выніку мы павінны атрымаць "як бы" усе магчымыя зыходы продажаў роўна сямі дзён, прычым з улікам частоты з’яўлення аднолькавых вынікаў.
Далей разбіваем увесь дыяпазон атрыманых значэнняў сум на адрэзкі у адпаведнасьці з той дакладнасцю, якая нам спатрэбіцца для вызначэння запасу. І будуем частотную гістаграму, якая як раз і пакажа рэальнае размеркаванне верагоднасцяў пакупак. У маім выпадку я атрымаў наступнае:
Паколькі ў мяне продажу штучнага тавару, г.зн. памер пакупкі заўсёды цэлы лік, то я і ня разбіваў на адрэзкі, пакінуў як ёсць. Вышыня слупка адпавядае долі агульных продажаў.
Як бачым, правая, "ненулевая9quot; частка разьмеркаваньня не нагадвае нармальнае размеркаванне (параўнайце з зялёным пункцірам).
Цяпер на падставе гэтага размеркавання нескладана разлічыць ўзроўні абслугоўвання, адпаведныя рознаму памеры запасу (SL1, SL2). Так што, задаўшы мэтавай ўзровень сэрвісу, адразу атрымлівае патрэбу запас.
Але і гэта не ўсё. Калі ўвесці ў разгляд фінансавыя паказчыкі — сабекошт, прагнозная цана, кошт утрымання запасу, лёгка лічыцца і прыбытковасць, адпаведная кожнаму памеры запасу і кожнаму ўзроўню сэрвісу. Яна ў мяне паказана ў апошняй калонцы, а адпаведныя графікі вось:
Гэта значыць тут мы даведаемся максімальна эфектыўны запас і ўзровень абслугоўвання з пункту гледжання атрымання прыбытку.
Напрыканцы (у чарговы ўжо раз) хочацца спытаць: "а чаму мы ўзровень абслугоўвання засноўвае на ABC-аналізе?" Здавалася б, у нашым выпадку аптымальны ўзровень сэрвісу першага роду складае 91% па-за залежнасці ад таго, у які з груп тавар знаходзіцца. Таямніца гэта вялікая ёсць.
Мадыфікацыя метаду Виллемейна для аптовых і падобных рынкаў
Некаторыя заўвагі аб аптовых і падобных рынках.
Нагадаю, што адно з дапушчэнняў, на якіх мы грунтаваліся — незалежнасць продажаў аднаго дня ад іншага. Гэта вельмі добрае дапушчэнне для розніцы. Напрыклад, чаканыя продажу хлеба сёння ніяк не залежаць ад яго учорашніх продажаў. Такая карцінка наогул характэрная там, дзе ёсць досыць вялікая кліенцкая база. Таму выпадкова абраныя тры дні могуць даць такі вынік
Зусім іншая справа, калі мы маем адносна няшмат кліентаў, асабліва калі яны купляюць нячаста і памногу. у гэтым выпадку верагоднасць падзеі, аналагічнага трэцяга варыянту, практычна нулявая. Выкладаючы простай мовай, калі ў мяне ўчора былі вялікія адгрузкі, хутчэй за ўсё сёння будзе зацішша. І ўжо зусім фантастычна выглядае варыянт, калі попыт будзе вялікі на працягу некалькіх дзён запар.
Значыць, незалежнасць продажаў суседніх дзён у гэтым выпадку можа апынуцца лухтой сабачай, і значна больш лагічна выказаць здагадку адваротнае — яны цесным чынам звязаныя. Што ж, нас гэтым не спалохаеш. Усяго-то толькі мы не будзем выдзіраць дні цалкам выпадкова, мы будзем браць дні, якія ідуць запар:
Ўсе нават цікавей. Паколькі шэрагі ў нас адносна кароткія, нам нават не трэба затлумляцца з выпадковай выбаркай — досыць прагнаць па шэрагу слізгальнае акно памерам у тэрмін рэакцыі, і гатовая гістаграма ў нас у кішэні.
Але тут ёсць і недахоп. Справа ў тым, што мы атрымліваем значна менш назіранняў. Для акна ў 7 дзён за год можна атрымаць 365-7 назіранняў, тады як пры выпадковай выбарцы 7 з 365 — гэта лік спалучэнняў 365! / 7! / (365-7)! Лічыць лянота, але гэта нашмат больш.
А малое колькасць назіранняў азначае ненадзейнасць адзнак, так што збірайце дадзеныя — яны лішнімі не бываюць!