Теорема синусов — теорема, которая устанавливает зависимость: стороны треугольника — противолежащие им углы.
Теорема синусов: Стороны треугольника пропорциональны синусам противолежащих углов.
Есть 2 подвида теоремы: обычная и расширенная теорема синусов.
Обычная теорема синусов:
Стороны треугольника пропорциональны sin противоположных углов.
Расширенная теорема синусов для произвольного треугольника:
где a, b, c — стороны треугольника, , β, γ — противолежащие этим сторонам углы, а R — радиус окружности, которая описана вокруг треугольника.
Доказательство теоремы синусов.
Пусть есть треугольник, вписанный в окружность. Обозначим его как ABC.
Что бы доказать всю теорему, так как треугольник имеет произвольные размеры, можно доказать только то, что соотношение 1-ной произвольной стороны к противолежащему углу соответствует 2R. Допустим, это будет 2R = a/sin , т.е. если смотреть по чертежу 2R = BC / sin A.
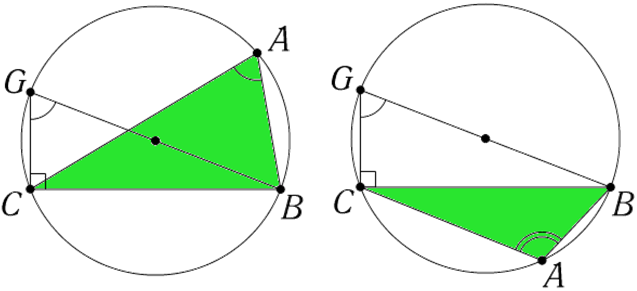
Проведем диаметр |BG| для описанной окружности. Из свойства углов, которые вписаны в окружность, угол GCB будет прямым, а угол CGB равен либо , когда точки A и G находятся по одну сторону от прямой BC, или − в противоположном варианте. Так как sin(−)=sin, в обоих случаях получаем:
a=2R sin
Повторяем это же рассуждение для оставшихся сторон треугольника:
Теорема синусов и косинцсов
Теоремы косинусов и синусов
Теорема косинусов . Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними.
Доказательство. Дан ∆АВС. Рассмотрим векторы , , (рис. 13). Очевидно , . Возведем это равенство скалярно в квадрат:
Используя теперь определение скалярного произведения векторов, имеем
, где , , — длины сторон ∆АВС, < A – угол между сторонами АВ и АС. Теорема доказана.
Теорема синусов. Стороны треугольника пропорциональны синусам противолежащих углов.
Доказательство. Рассмотрим ∆АВС со сторонами a , b , c и противолежащими углами &#&45; , &#&46; , &#&47; . Докажем, что
.
Из вершины С треугольника АВС опустим высоту CD . Из прямоугольного ∆АС D , если &#&45; – острый угол, получаем . Если &#&45; – тупой угол, то .
Аналогично из прямоугольного ∆ BCD получаем . Таким образом, , т.е. . Опуская высоту в треугольнике АВС из вершины А , аналогично имеем . Итак, .
Очевидно, что эта формула справедлива в случае прямоугольного треугольника АВС.