Тригонометрические функции: (sin alpha ), (cos alpha ), (tan alpha ), (cot alpha ), (sec alpha ), (csc alpha )

Множество действительных чисел: (mathbb)

Координаты точки окружности: (x), (y)

Тригонометрические функции представляют собой элементарные функции, аргументом которых является угол . С помощью тригонометрических функций описываются соотношения между сторонами и острыми углами в прямоугольном треугольнике . Области применения тригонометрических функций чрезвычайно разнообразны. Так, например, любые периодические процессы можно представить в виде суммы тригонометрических функций ( ряда Фурье ). Данные функции часто появляются при решении дифференциальных и функциональных уравнений.

К тригонометрическим функциям относятся следующие 6 функций: синус , косинус , тангенс , котангенс , секанс и косеканс . Для каждой из указанных функций существует обратная тригонометрическая функция .

Геометрическое определение тригонометрических функций удобно ввести с помощью единичного круга . На приведенном ниже рисунке изображен круг радиусом (r = 1). На окружности обозначена точка (Mleft( right)). Угол между радиус-вектором (OM) и положительным направлением оси (Ox) равен (alpha).

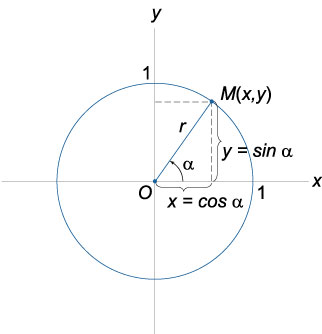
Синусом угла (alpha) называется отношение ординаты (y) точки (Mleft( right)) к радиусу (r):

Поскольку (r = 1), то синус равен ординате точки (Mleft( right)).

Косинусом угла (alpha) называется отношение абсциссы (x) точки (Mleft( right)) к радиусу (r):

Тангенсом угла (alpha) называется отношение ординаты (y) точки (Mleft( right)) к ee абсциссе (x):

Котангенсом угла (alpha) называется отношение абсциссы (x) точки (Mleft( right)) к ее ординате (y):

Секанс угла (alpha) − это отношение радиуса (r) к абсциссе (x) точки (Mleft( right)):

(sec alpha = r/x = 1/x,;;x ne 0)

Косеканс угла (alpha) − это отношение радиуса (r) к ординате (y) точки (Mleft( right)):

(csc alpha = r/y = 1/y,;;y ne 0)

В единичном круге проекции (x), (y) точки (Mleft( right)) и радиус (r) образуют прямоугольный треугольник, в котором (x,y) являются катетами, а (r) − гипотенузой. Поэтому, приведенные выше определения тригонометрических функций в приложении к прямоугольному треугольнику формулируются таким образом:

Синусом угла (alpha) называется отношение противолежащего катета к гипотенузе.

Косинусом угла (alpha) называется отношение прилежащего катета к гипотенузе.

Тангенсом угла (alpha) называется противолежащего катета к прилежащему.

Котангенсом угла (alpha) называется прилежащего катета к противолежащему.

Секанс угла (alpha) представляет собой отношение гипотенузы к прилежащему катету.

Косеканс угла (alpha) представляет собой отношение гипотенузы к противолежащему катету.

График функции синус

(y = sin x), область определения: (x in mathbb), область значений: (-1 le sin x le 1)

График функции косинус

(y = cos x), область определения: (x in mathbb), область значений: (-1 le cos x le 1)

График функции тангенс

(y = tan x), область определения: (x in mathbb, x ne left( <2k + 1>right)pi/2), область значений: (- infty < tan x < infty)

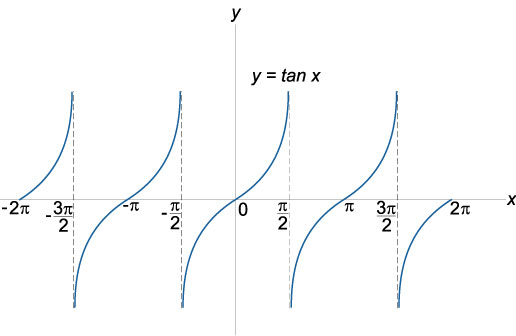
График функции котангенс

(y = cot x), область определения: (x in mathbb, x ne kpi), область значений: (- infty < cot x < infty)

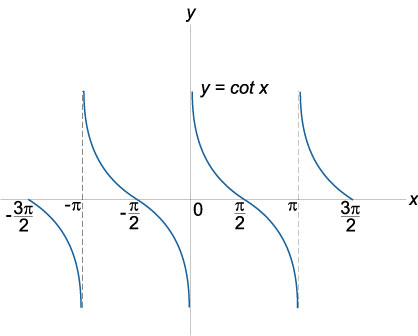
График функции секанс

(y = sec x), область определения: (x in mathbb, x ne left( <2k + 1>right)pi/2), область значений: (sec x in left( <-infty , -1>right] cup left[ <1,infty >right))

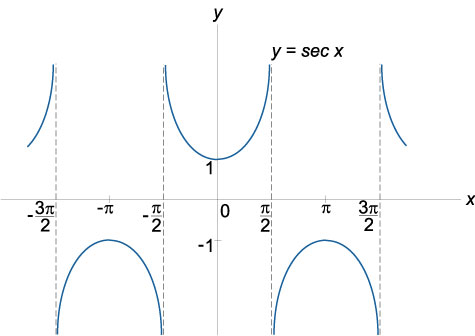
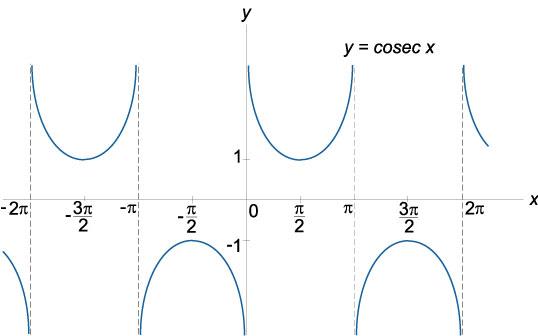
График функции косеканс

(y = csc x), область определения: (x in mathbb, x ne kpi), область значений: (csc x in left( <-infty , -1>right] cup left[ <1,infty >right))

Сайт оптимизирован для Chrome, Firefox, Safari и Internet Explorer.

Тригонометрических функций

ЧЕТНОСТЬ И ПЕРИОДИЧНОСТЬ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ.

Четность тригонометрических функций.

Четность тригонометрических функций.

Углы φ и —φ образуются при повороте луча в двух взаимно противоположных направлениях (по часовой стрелке и против часовой стрелки).

Поэтому конечные стороны OA ₁ и ОА ₂ этих углов симметричны относительно оси абсцисс.

Следовательно, синус является нечетной, а косинус — четной функцией угла.

Поэтому тангенс и котангенс являются нечетными функциями угла.

Выяснить, какие из данных функций являются четными и какие нечетными:

Периодичность функций sin φ и cos φ

Предположим, что вектор ОА = (х, у) единичной длины образует с осью абсцисс угол φ.

Если сделать полный оборот вектора ОА вокруг точки О против часовой стрелки, то получится угол φ + 360°. Но вектор ОА при этом займет первоначальное положение, а потому координаты его х и у не изменятся.

Эти соотношения показывают, что значения функций sin φ и cos φ не изменяются, если их аргумент, увеличить на 360°.

Пусть f(х) есть некоторое выражение, зависящее от переменной величины х.

Определяет у как функцию аргумента х.

Если при любых допустимых значениях аргумента х

где Т — некоторое отличное от нуля число, то функция f (x) называется периодической, а число Т — ее периодом.

Согласно этому определению функции sin x и cos х являются периодическими с периодом Т = 360°.

При n полных оборотах вектора ОА против часовой стрелки образуется угол φ + 360°n, а по часовой стрелке — угол φ — 360°n. В каждом из этих случаев координаты х и у вектора не изменяются, а потому не изменяются sin φ и cos φ.

где n — любое целое число (положительное, отрицательное или нуль).

Формулы (1) показывают, что каждый из углов

является периодом функции sin φ и cos φ. Таким образом, эти периодические функции имеют бесконечное множество периодов.

Можно доказать, что любая периодическая функция (а не только sin φ и cos φ) имеет бесконечное множество периодов.

Говоря о периоде функции, удобно из бесконечного множества всех ее периодов иметь в виду какой-нибудь один вполне определенный период. Обычно выделяют наименьший положительный период функции.

Из всех рассмотренных выше периодов функции sin φ наименьшим положительным периодом является угол в 360°. Но, может быть, существует еще меньший угол, который мы просто упустили из виду, но который, Также является периодом функции sin φ? Чтобы решить этот вопрос, предположим, что наименьший положительный период функции sin φ равен Т. Тогда при любом φ

Но нулю равны синусы лишь тех положительных углов, которые кратны углу в 180° , то есть углов в 180°, 360°, 540° и т. д. Поэтому единственным «конкурентом9raquo; для угла » 360° является угол в 180°.

Составляет ли он период функции sin φ? Если бы это было так, то равенство sin (φ + 180°) = sin φ должно было бы выполняться при всех значениях φ. В частности, при φ = &09deg; мы получили бы

Ho sin 270° = —1, a sin &09deg; = 1 . Поэтому угол в 180° не является периодом функции sin φ. Остается признать, что периодом (то есть наименьшим положительным периодом) функции sin φ является угол в 360°.

Аналогично можно доказать, что периодом функции cos φ также является угол в 360° Предлагаем учащимся убедиться в этом самостоятельно.

1. Доказать следующие соотношения:

а) sin 740° = sin 20°; в) cos 54° = cos (—1026°);

2. Данные выражения преобразовать так, чтобы входящие в них углы были положительными и не превышали 360°:

3. Данные выражения преобразовать так, чтобы входящие в них углы по абсолютной величине не превышали 180°:

a) cos 72&9deg;; б) sin 1268°; в) sin (— 535°); г) cos (— 1001°).

4. Доказать, что угол в 540° является одним из периодов функции у = cos2х.

5. Доказать, что угол и 360° является одним из периодов функции у = tgx.

6. Докажите, что любой период Т функции у = cos х является корнем уравнения

Верно ли обратное утверждение?

Периодичность функций tg φ и ctg φ

Мы знаем, что тангенс угла φ равен ординате соответствующей точки В на оси тангенсов . При повороте вектора ОА , образующего с осью абсцисс угол φ, на 180° против часовой стрелки вектор изменит свое направление на противоположное, но соответствующая точка В на оси тангенсов останется прежней. Поэтому не изменится и тангенс угла.

Следовательно, при любом φ

Это означает, что функция tg φ является периодической с периодом 180°. Но будет ли угол в 180° наименьшим жительным периодом этой функции?

Предположим, что наименьший положительный период функции tg φ равен Т. Тогда для всех допустимых значений φ должно быть

В частности, при φ = 0° получаем:

Но тангенс положительного угла равен нулю лишь тогда, когда синус этого угла равен нулю, то есть при Т = 180°, 360°, 540° и т, д. Следовательно, никакой положительный угол, меньший 180°, не может быть периодом функции tg φ. Остается признать, чтб периодом (то есть наименьшим положительным периодом) функции tg φ является угол в 180°.

Аналогично можно доказать, что периодом функции сtg φ также является угол в 180°. Предлагаем учащимся убедиться в этом самостоятельно.

1. Данные выражения преобразовать так, чтобы входящие в них углы были положительными и не превышали 180°:

2. Данные выражения преобразовать так, чтобы входящие в них углы по абсолютной величине не превышали &09deg;:

3. Доказать, что угол в 120° является одним из периодов функции у = ctg 3х.

4. Доказать, что любой период Т функции у = ctg х является корнем уравнения

Верно ли обратное утверждение?

О периодических функциях.

Если функция f(x) периодична с периодом Т, то по значениям этой функции на любом отрезке длины Т можно восстановить ее значения на всей числовой прямой.

Действительно, пусть периодическая функция f(x) задана в интервале (а, а + Т), где Т — период этой функции.

Покажем, как можно определить значения этой функции в интервале ( а + Т, а + 2 T ).

Для любой точки b из этого интервала можно указать точку b‘ из интервала (а, а + T ), отстоящую от b на расстоянии T.

В силу периодичности функции f(x)

Таким образом, по заданным значениям функции f в интервале (а, а +T ) можно восстановить значения этой функции в интервале (а + Т, а + 2T ). Затем исходя из значений функции f в интервале (а + Т, а + 2T ), можно восстановить ее значения в интервале (а + 2T, а + 3T ). После этогo точно так же можно найти значения функции f в интервале (а + 3T, а + 4T) и т. д. Аналогично можно определить значения функции f(x) и во всех точках числовой прямой, лежащих левее отрезка (а, а + Т ).